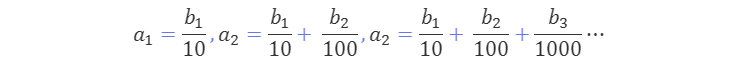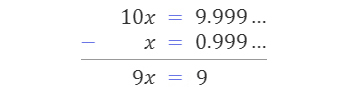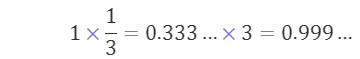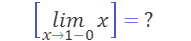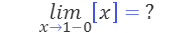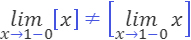수학의 세계(0.999...는 1일까?)

“1나누기 3은 0.333…. 0.333… 곱하기 3은 0.999…. 그런데, 1/3곱하기 3은 1? 그러면 0.999…는 1? 0.999…가 1과 같다고? 0.999…는 1보다 작을 것 같은데? 아주 아주 아주 조금이라도 작지 않나? 그런데 1하고 같다고? 끊임없이 반복되는 0.999…와 관련된 의문에 마침표를 찍어본다.”

 

“무한”이 관련된 문제는 사람들의 호기심을 자극하면서 한편으론 사람들을 무척 혼란스럽게 만든다. 무한소수와 관련된 0.999… = 1이 대표적인 예이다. 유한의 사고방식에 익숙한 사람에게는 이상해 보일 수도 있고 이해가 어렵기도 하다. 그러다 보니, 이상한 논리를 내세우고 자기 주장이 옳다고 싸우기까지 하는 일이 많아, 수학 분야의 영원한 ‘떡밥’이라고 할 수 있다. 0.999… = 1인 이유를 설명하기에 앞서 왜 0.999…가 1이 아닌 것처럼 느껴지는지 두 가지 정도의 이유를 살펴보자.

 

첫 번째 이유는 귀납적인 방식을 잘못 사용하여, 유한한 것을 다룰 때의 사고 방식을 무한의 상황에도 비판 없이 적용하기 때문이다. 물론 0.9는 1보다 작고, 0.99도 1보다 작고, 0.999도 1보다 작다. 이런 식으로 9를 아무리 반복해도 1보다 작으니, 0.999… 또한 1보다 작아야 한다고 생각하는 것이다. 그러나 위의 관찰은 사실 9가 유한하게 이어지는 0.999…9는 1보다 작고, 이런 경우는 무한히 많다라는 것에 불과하다. 이를 근거로 9가 무한 개인 0.999…9는 1보다 작다고 말하는 것은 오류이다. 이해를 돕기 위해 다음과 같은 예를 생각해 보자.     이와 같이 무한히 많은 유한한 상황에 대해 어떤 성질이 성립한다고 해서, 일반적으로 상황 자체가 무한한 경우까지 그 성질이 그대로 유지되는 것은 아니다. 0.999…가 1보다 작은지 그렇지 않은지도 마찬가지이다.

 

두 번째 이유로는, 수에 대해 모호한 개념을 가지고 있기 때문이다. 달리 표현하면 무한 소수의 정의를 정확히 모르기 때문이다. 그렇다 보니, 0.999…를 1에 한없이 다가가며 움직이는 그 무엇으로 생각하는 경우가 많다. 0.999…는 수냐고 물어보면 “수는 아니고, 수와 비슷한 것”과 같은 이상한 답변을 하는 일도 있다. 혹은 “0.999…는 1이 아니지만, 그 차이가 아주 작으므로 편의상 0.999… = 1이라고 둔다” 는 식의 잘못된 설명을 하기도 한다.

 

0.999… = 1인 이유를 설명하는 방법도 대단히 많은데 그 중 하나가 실수의 대소 관계를 이용하는 설명이다. 0.999… ≠1 이라고 주장하는 사람은 0.999… < 1이라고 주장하는 셈이다. 그런데, 두 실수 a, b 에 대해 “a < b라는 것”과 “a < c < b인 실수 c를 찾을 수 있다는 것”은 똑같은 얘기이다. 특히, c = (a+b)/2 가 그런 성질을 만족하기 때문이다. (예를 들어 2가 3보다 작으므로, 두 수의 평균 2.5는 2보다 크고 3보다 작다) 따라서 0.999… ≠ 1이라는 주장은 0.999…보다 크고, 1보다 작은 수 c를 찾을 수 있다는 주장과 똑같은 주장이다. 이런 수를 찾을 수 있을까? 당연히 찾을 수 없다. 0.999…와 1의 평균 c = (0.999… + 1)/2를 구하면 되지 않느냐고 생각할 수도 있겠지만, 그렇다면 c를 소수로 나타내면 어떤 수가 될까? 0.999…5일까? “끝자리가 없는” 수 0.999… 의 ‘끝자리’에 수를 붙일 수가 있을까?

 

불행히도 그런 것은 수가 아니다. 0.999…는 소수점 아래로 9가 끝이 없이 이어지는 수라고 해 놓고, 맨 ‘끝’에 숫자를 더 붙인다는 것은 반칙이다. 백 번 양보해서 그런 것도 수라고 인정해 주더라도, 이 수가 0.999…보다 클 것 같지도 않다.   똑같은 말이지만, 1에서 0.999…를 빼보기로 하자. 뺄셈 결과는 소수점 아래에 0이 무한히 반복되므로 그냥 0과 같다! 누군가 이 뺄셈의 결과를 0.000…1이라고 주장한다면 역시 반칙을 저지르는 것이다.

 

순환소수를 분수로 고치는 방법을 이용하여 보자. x = 0.999…라고 두고 양변을 10배 하면, 10x = 9.999…이다. 따라서, 두 식의 양변을 각각 빼면,

 

이므로 양변을 9로 나누어 x=1을 얻는 것이다. 이 계산에 대해서도 마음이 불편한 사람이 많다. 10x의 소수점 아래의 9의 개수가, x의 소수점 아래의 9의 ‘개수’보다 하나 적어 보인다는 주장이다. 따라서 뺄셈을 한 결과는 9가 아니라 8.999… 혹은 8.999…1이라고 주장하기도 한다.

 

뒤쪽 계산 결과가 나온다는 주장은 ‘끝자리가 없는’ 수 0.999… 의 ‘끝자리’에 수를 붙인 것이니 앞서 말한 대로 반칙이다. 첫 번째 계산 결과를 주장하는 사람은 소수점 이하의 9의 개수에 민감한 사람인 것 같다. 그러니 9x = 8.999…에서 소수점 이하의 9의 개수가, x = 0.999…의 소수점 이하의 9의 개수와 같은지 분명히 해두면 된다. 아니면 10x = 9.999…의 소수점 이하의 9의 개수와 같은지 분명히 해보자. (둘 다 아니라면? 먼저 개수가 무엇인지부터 제대로 정의하길) x의 소수점 이하의 9의 개수와 같다면, 9x = 8.999…의 양변에서 x를 빼주어 8x = 8, 즉, x=1에 아무런 불만이 없을 것이다. 10x의 소수점 이하의 9의 개수와 같다면, 10x = 9.999…에서 9x = 8.999…를 변끼리 빼주면 x=1을 얻게 되는 것에 불만이 없을 것이다.

 

1/3 = 0.333…는 대부분 인정할 것이다. (이것마저 인정하지 않는다는 것은, 무한소수를 자기 맘대로 이해하고 있다는 뜻이지만…) 양변에 3을 곱하면, 오른쪽과 같으므로 깔끔하다.

 

이에 대해 무한소수를 3배 하는 것이 불가능하다, 혹은 무한소수는 수가 아니라는 식의 주장을 하기도 한다. ⅓이 나 원주율 π등의 무한소수를 수로 생각하고 연산해 온 것이 몇 천 년이고, 그 동안 이런 수를 더하고, 곱하고, 빼고, 0이 아닌 것으로 나누는 일은 아무 문제없이 인류가 해 온 일이다. 물론 수학적으로도 무한소수에 대한 이론은 잘 정립되어 있다. 무한소수를 두려운 대상으로 생각한 나머지 연산이 잘못 됐다든지, 수가 아니라는 주장은 번지수를 확실히 잘못 짚은 것이다.

이제  좀더 수학적인 설명을 하는 동시에 0.999…가 도대체 무엇인지, 더 나아가 수학자들은 무한소수를 어떻게 정의하는지 알아보려고 한다. 어떤 수열 an 이 L이라는 숫자로 다가간다는 것은 n이 클수록 L과 an 의 오차가 0에 가까워진다는 것이다. 이 때, limn→∞an 을 L이라고 쓰기로 약속한다. b1, b2, …가 0부터 9까지의 정수일 때 대응하는 다음과 같은 수열을 생각해 보자.

 

 

이 수열이  다가가는 숫자 L을 무한소수 0.b1b2b3 …로 쓰기로 약속한다. 즉, L = 0.b1b2b3…이다. b1 = b2 = b3 = … = 9일 때, 대응하는 수열은 a1 = 0.9, a2 = 0.99, a3 = 0.999, a4 = 0.9999, …이다. 이제 이 수열 an이 L로 다가가면, L = 0.999…일 것이다. 그런데 이 수열은 1로 다가가는 것을 쉽게 알 수 있다. 왜냐하면, 1 과 an의 오차는 0.1, 0.01, 0.001, …인데 이 값이 0에 가까워지기 때문이다. 따라서 1 = 0.999…이다.

 

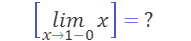
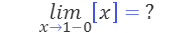
0.999…=1에 꼭 따라 나오는 질문이 있다. 주어진 수 x에 대하여 x보다 크지 않은 정수 중 가장 큰 정수를 [ x ]라고 쓸 때, [0.999…]의 값이 얼마인지를 묻는 것이다. 0.999… = 1이므로 당연히 [0.999…] = [1] = 1이다. 이 질문은 1보다 작은 쪽에서 1에 무한히 가까이 다가갈 때의 값을 묻는 셈이니까, 고등학교에서 배우는 좌극한 기호를 이용하면 이렇게 생각할 수 있다.   그렇다면, 극한과 [ ]의 순서를 바꾼다면 어떨까?     첫 번째 식은 0.9, 0.99, 0.999, …가 다가가는 수보다 크지 않은, 즉 1보다 크지 않은 가장 큰 정수가 되므로 그 값이 1인 반면, 두 번째 식은 [0.9] = 0, [0.99] = 0, [0.999] = 0, …이 다가가는 수니까 그 값은 0이다. [0.999…]를 0이라고 착각하는 것은, 위의 두 식을 같은 것으로 혼동하기 때문이다. 일반적으로 ‘극한값을 구한 다음의 함숫값’과 ‘함숫값을 구한 다음의 극한값’은 다르다. 이 두 값이 같을 때, 우리는 그 함수를 ‘연속함수’라고 부른다. 즉, 연속함수는 함수와 극한의 위치를 바꿀 수 있는 함수라고 할 수 있다. 이 질문의 경우 f(x) = [x]라는 함수의 그래프를 생각하면, 함수 f(x)는 x가 정수일 때 언제나 불연속이 됨을 알 수 있다. 그러므로 아래와 같다.

 

 

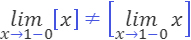
정말 어렵군요,,,.' 

 

 




http://navercast.naver.com/science/math/22